Deconstructing Neoclassical Utility
Several commenters have pointed out definitional problems with the term “utility” as used in neoclassical economics, including Tarheel Dem, rg and Alan. As I noted in the linked post, Samuelson and Nordhaus are careful to call utility a “ scientific construct”, and not a measurable thing. Philip Mirowski is very helpful in clarifying what this remarkable notion might mean. I’ve referred several times to this paper, Physics and the “Marginalist Revolution”, in which Mirowski offers a brief, perhaps too brief, explanation, which he incorporated into a dense, perhaps too dense, book, More Heat Than Light: Economics as Social Physics, Physics as Nature’s Economics. I’m slowly making my way through the book, but the paper is probably enough for a decent understanding of one issue.
Mirowski says that the four most important neoclassical economists were hooked on the physics of the day. All of them, Jevons, Pareto, Walras and Edgeworth, were trained in math and physics, and all had at least some acquaintance with the work of Jeremy Bentham. They were also quite explicit that their ideas were congruent with the emerging understanding of energy as a mathematical basis for a number of expanding areas of physics. He quotes Jevons as follows:
Utility only exists when there is on the one side the person wanting, and on the other the thing wanted… Just as the gravitating force of a material body depends not alone on the mass of that body, but upon the masses and relative positions and distances of the surrounding material bodies, so utility is an attraction between a wanting being and what is wanted. Citation omitted.
Jevons repeatedly uses language suitable to calculus to explain his derivation of economic laws. He refers to the effect of the increase in utility that comes from the addition of an “infinitesimal” increase in the amount of the commodity consumed; the use of that term, which could not possibly arise in the real world, is intended to make it appear that standard integration rules are applicable to his theory, and he draws smooth curves instead of stairstep lines to show the consumption of goods and services. Samuelson and Nordhaus do the same thing, though a bit more subtly. Economics, 2005 ed.
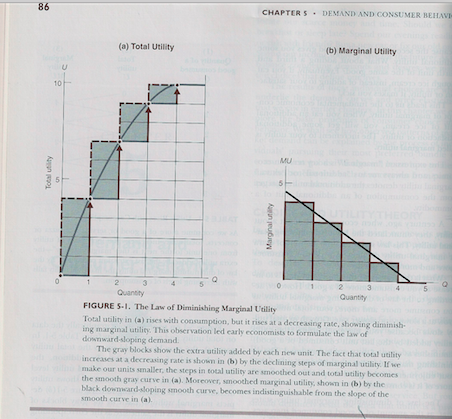
This is hardly the only inaccurate use of math. Consider this drawing from the Mirowski paper:
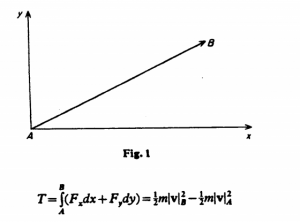
In this picture there is a point particle moved from point A to point B in a two-dimensional plane by a force F (vectors are usually indicated by bold-face; I’m also using italics). We can rewrite F as the combination of Fx and Fy the components of the force vector along the x and y axes. For a quick brush-up on this point, see this. The equation in the drawing gives the kinetic energy of the particle, denoted by T. If the expression Fxdx + Fydy is an exact differential, then there is another function U that meets this requirement:
![]()
The U in this equation is identified as the potential energy of the particle. The particle moves along a path such that the sum of T and U remains constant; usually this is written as T – U = 0. The point of Mirowski’s example is that we are looking at a force field, an energy field that describes the energy at each point by amount and direction. The function F does not have to be a simple equation as it would be in the first example; it can map out complicated curves. But F and each of its components have to be the exact differential of some other equation, which puts some constraints on them. Finally, we should note that this idea can be generalized to any number of dimensions.
This is from the Mirowski paper:
Walras insisted that his … equations resembled those of the physical sciences in every respect. We may see now that he was very nearly correct. Simply redefine the variables of the earlier equations: let F be the vector of prices of a set of traded goods, and let q be the vector of the quantities of those goods purchased. The integral ∫F•dq = T is then defined as the total expenditure on those goods. If the expression to be integrated is an exact differential, then it is possible to define a scalar function of the goods x and y of the form U = U(x,y), which can then be interpreted as the “utilities of those goods. In exact parallel to the original concept of potential energy, these utilities are unobservable, and can only be inferred from theoretical linkage to other observable variables. P. 368
In other words, utility is a scientific construct. I hope this from the book will make this somewhat clearer.
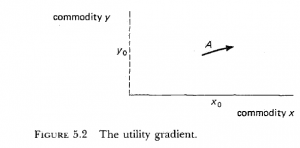
Suppose we have a person with a supply of two goods that can be traded, designated by x0 and y0. The point A is the intersection of the two goods. In neoclassical economics world, our hypothetical person is presumed to know how much of each good the person would purchase with an infinitesimal increase in money. The person is presumed to know this for every point in the commodity plane. This example can also be expanded into multiple dimensions to cover multiple commodities.
The math goes on from here, but we don’t really need to follow it. We can see that this doesn’t really make good sense, the idea that we would know what to do with an infinitesimal part of a piece of money. But even the math doesn’t make sense, as Mirowski explains in tedious detail. The equations aren’t solvable unless there are certain kinds of constraints. The physics problem is solved by assuming that the energy of the system is conserved, or at least it was when Walras and Jevons were writing, and we still use that idea today for simple local problems, like mechanics in physics. But that constraint isn’t available in economics: T is the equivalent of money, and U is utility, and the two are measured in different units. The term T – U doesn’t mean anything. Neither do other possible constraints, as Mirowski explains. The math fails at every level, including the levels Mirowski plumbs and I won’t.
One of the problem this creates for economics is that it undermines the claim that markets are demonstrably a superior form of organization. Recall from this post that Jevons makes this claim explicit. There are other problems, as Mirowski explains in section 5 of the paper and at much greater length in the book.
The standard response to the deconstruction of the basis of the model is to say it doesn’t matter. The models work, so who cares how or why. This was Milton Friedman’s view, as in this excerpt from Essays From Positive Economics from 1953. This raises a host of fascinating questions, but for now, here are two thoughts.
1. Lots of important problems can be solved with simple Newtonian analysis. If I want to figure out how a ball will roll down a ramp or how the moon revolves around the earth, I don’t need anything more complicated to get really close to the correct answers. But there are many other problems for which relativity theory is necessary. There are others that cannot be solved without quantum mechanics. The fact that some kinds of economic problems can be solved with simple neoclassical models doesn’t mean that all economics works that way, or that there might not be other and much better ways to figure out how to organize a society for production and allocation of scarce resources.
2. Economics is not a normative field. The rules of a society must deal not only with economic efficiency and utility of individuals at a point in time, which seem to be the subjects of neoclassical market theory, but many and broader aspects of being human, including our interest in the future, the impacts of our behavior on other people, fairness, social justice, and a host of other concerns. The neoliberal program seeks to erase those concerns in search of homo economicus, the consuming person, as the sole exemplar and highest form of being human. When we talk about society, we are told by Margaret Thatcher that there is no such thing. Not only is there a society, there is a government, which is a tool for society to arrange things as we see fit. We don’t have to live like the solitary selfish solipsistic homo economicus. We have plenty of choices.
